How to analyze data using anova in MS excel?

How to Analyse Data Using Anova in Ms Excel 

Regression Analysis: Overview

Overview

Suppose you’re a sales manager trying to predict next month’s numbers. You know that dozens, perhaps even hundreds of factors from the weather to a competitor’s promotion to the rumor of a new and improved model can impact the number. Perhaps people in your organization even have a theory about what will have the biggest effect on sales. “Trust me. The more rain we have, the more we sell.” “Six weeks after the competitor’s promotion, sales jump.” To answer is the use of regression analysis.

While there are many types of regression analysis, at their core they all examine the influence of one or more independent variables on a dependent variable.

What is regression analysis and what does it mean to perform a regression?

Regression analysis is a powerful statistical method that allows you to examine the relationship between two or more variables of interest. 

Regression analysis is a way of mathematically sorting out which of those variables does indeed have an impact. It answers the questions: Which factors matter most? Which can we ignore? How do those factors interact with each other? And, perhaps most importantly, how certain are we about all of these factors?

Regression analysis is a reliable method of identifying which variables have impact on a topic of interest. The process of performing a regression allows you to confidently determine which factors matter most, which factors can be ignored, and how these factors influence each other.

In order to understand regression analysis fully, it’s essential to comprehend the following terms:

Dependent Variable: This is the main factor that you’re trying to understand or predict. 

Independent Variables: These are the factors that you hypothesize have an impact on your dependent variable.

In our application training example above, attendees’ satisfaction with the event is our dependent variable. The topics covered, length of sessions, food provided, and the cost of a ticket are our independent variables.

How does regression analysis work?

In order to conduct a regression analysis, you’ll need to define a dependent variable that you hypothesize is being influenced by one or several independent variables.

You’ll then need to establish a comprehensive dataset to work with. Administering surveys to your audiences of interest is a terrific way to establish this dataset. Your survey should include questions addressing all of the independent variables that you are interested in.

Let’s continue using our application training example. In this case, we’d want to measure the historical levels of satisfaction with the events from the past three years or so (or however long you deem statistically significant), as well as any information possible in regards to the independent variables. 

Perhaps we’re particularly curious about how the price of a ticket to the event has impacted levels of satisfaction. 

To begin investigating whether or not there is a relationship between these two variables, we would begin by plotting these data points on a chart, which would look like the following theoretical example.

(Plotting your data is the first step in figuring out if there is a relationship between your independent and dependent variables)

Our dependent variable (in this case, the level of event satisfaction) should be plotted on the y-axis, while our independent variable (the price of the event ticket) should be plotted on the x-axis.

Once your data is plotted, you may begin to see correlations. If the theoretical chart above did indeed represent the impact of ticket prices on event satisfaction, then we’d be able to confidently say that the higher the ticket price, the higher the levels of event satisfaction. 

But how can we tell the degree to which ticket price affects event satisfaction?

To begin answering this question, draw a line through the middle of all of the data points on the chart. This line is referred to as your regression line, and it can be precisely calculated using a standard statistics program like Excel.

We’ll use a theoretical chart once more to depict what a regression line should look like.

The regression line represents the relationship between your independent variable and your dependent variable. 

Excel will even provide a formula for the slope of the line, which adds further context to the relationship between your independent and dependent variables. 

The formula for a regression line might look something like Y = 100 + 7X + error term.

This tells you that if there is no “X”, then Y = 100. If X is our increase in ticket price, this informs us that if there is no increase in ticket price, event satisfaction will still increase by 100 points. 

You’ll notice that the slope formula calculated by Excel includes an error term. Regression lines always consider an error term because in reality, independent variables are never precisely perfect predictors of dependent variables. This makes sense while looking at the impact of ticket prices on event satisfaction — there are clearly other variables that are contributing to event satisfaction outside of price.

Your regression line is simply an estimate based on the data available to you. So, the larger your error term, the less definitively certain your regression line is.

Why should your organization use regression analysis?

Regression analysis is helpful statistical method that can be leveraged across an organization to determine the degree to which particular independent variables are influencing dependent variables.

The possible scenarios for conducting regression analysis to yield valuable, actionable business insights are endless.

The next time someone in your business is proposing a hypothesis that states that one factor, whether you can control that factor or not, is impacting a portion of the business, suggest performing a regression analysis to determine just how confident you should be in that hypothesis! This will allow you to make more informed business decisions, allocate resources more efficiently, and ultimately boost your bottom line.

Source: BEN FOLEY - https://www.surveygizmo.com/resources/blog/regression-analysis

An Interactive Guide To The Fourier Transform

An Interactive Guide To The Fourier Transform

The Fourier Transform is one of the deepest insights ever made. Unfortunately, the meaning is buried within dense equations:

Yikes. Rather than jumping into the symbols, let's experience the key idea firsthand. Here's a plain-English metaphor:

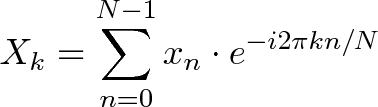
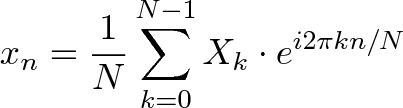
• What does the Fourier Transform do? Given a smoothie, it finds the recipe.
• How? Run the smoothie through filters to extract each ingredient.
• Why? Recipes are easier to analyze, compare, and modify than the smoothie itself.
• How do we get the smoothie back? Blend the ingredients.

Here's the "math English" version of the above:

• The Fourier Transform takes a time-based pattern, measures every possible cycle, and returns the overall "cycle recipe" (the amplitude, offset, & rotation speed for every cycle that was found).

Time for the equations? No! Let's get our hands dirty and experience how any pattern can be built with cycles, with live simulations.

If all goes well, we'll have an aha! moment and intuitively realize why the Fourier Transform is possible. We'll save the detailed math analysis for the follow-up.

This isn't a force-march through the equations, it's the casual stroll I wish I had. Onward!

From Smoothie To Recipe

A math transformation is a change of perspective. We change our notion of quantity from "single items" (lines in the sand, tally system) to "groups of 10" (decimal) depending on what we're counting. Scoring a game? Tally it up. Multiplying? Decimals, please.

The Fourier Transform changes our perspective from consumer to producer, turning What do I have? into How was it made?

In other words: given a smoothie, let's find the recipe.

Why? Well, recipes are great descriptions of drinks. You wouldn't share a drop-by-drop analysis, you'd say "I had an orange/banana smoothie". A recipe is more easily categorized, compared, and modified than the object itself.

So... given a smoothie, how do we find the recipe?

Well, imagine you had a few filters lying around:

• Pour through the "banana" filter. 1 oz of bananas are extracted.
• Pour through the "orange" filter. 2 oz of oranges.
• Pour through the "milk" filter. 3 oz of milk.
• Pour through the "water" filter. 3 oz of water.

We can reverse-engineer the recipe by filtering each ingredient. The catch?

• Filters must be independent. The banana filter needs to capture bananas, and nothing else. Adding more oranges should never affect the banana reading.
• Filters must be complete. We won't get the real recipe if we leave out a filter ("There were mangoes too!"). Our collection of filters must catch every possible ingredient.
• Ingredients must be combine-able. Smoothies can be separated and re-combined without issue (A cookie? Not so much. Who wants crumbs?). The ingredients, when separated and combined in any order, must make the same result.

See The World As Cycles

The Fourier Transform takes a specific viewpoint: What if any signal could be filtered into a bunch of circular paths?

Whoa. This concept is mind-blowing, and poor Joseph Fourier had his idea rejected at first. (Really Joe, even a staircase pattern can be made from circles?)

And despite decades of debate in the math community, we expect students to internalize the idea without issue. Ugh. Let's walk through the intuition.

The Fourier Transform finds the recipe for a signal, like our smoothie process:

• Start with a time-based signal
• Apply filters to measure each possible "circular ingredient"
• Collect the full recipe, listing the amount of each "circular ingredient"

Stop. Here's where most tutorials excitedly throw engineering applications at your face. Don't get scared; think of the examples as "Wow, we're finally seeing the source code (DNA) behind previously confusing ideas".

• If earthquake vibrations can be separated into "ingredients" (vibrations of different speeds & amplitudes), buildings can be designed to avoid interacting with the strongest ones.
• If sound waves can be separated into ingredients (bass and treble frequencies), we can boost the parts we care about, and hide the ones we don't. The crackle of random noise can be removed. Maybe similar "sound recipes" can be compared (music recognition services compare recipes, not the raw audio clips).
• If computer data can be represented with oscillating patterns, perhaps the least-important ones can be ignored. This "lossy compression" can drastically shrink file sizes (and why JPEG and MP3 files are much smaller than raw .bmp or .wav files).
• If a radio wave is our signal, we can use filters to listen to a particular channel. In the smoothie world, imagine each person paid attention to a different ingredient: Adam looks for apples, Bob looks for bananas, and Charlie gets cauliflower (sorry bud).

The Fourier Transform is useful in engineering, sure, but it's a metaphor about finding the root causes behind an observed effect.

Think With Circles, Not Just Sinusoids

One of my giant confusions was separating the definitions of "sinusoid" and "circle".

• A "sinusoid" is a specific back-and-forth pattern (a sine or cosine wave), and 99% of the time, it refers to motion in one dimension.
• A "circle" is a round, 2d pattern you probably know. If you enjoy using 10-dollar words to describe 10-cent ideas, you might call a circular path a "complex sinusoid".

Labeling a circular path as a "complex sinusoid" is like describing a word as a "multi-letter". You zoomed into the wrong level of detail. Words are about concepts, not the letters they can be split into!

The Fourier Transform is about circular paths (not 1-d sinusoids) and Euler's formula is a clever way to generate one:

Must we use imaginary exponents to move in a circle? Nope. But it's convenient and compact. And sure, we can describe our path as coordinated motion in two dimensions (real and imaginary), but don't forget the big picture: we're just moving in a circle.

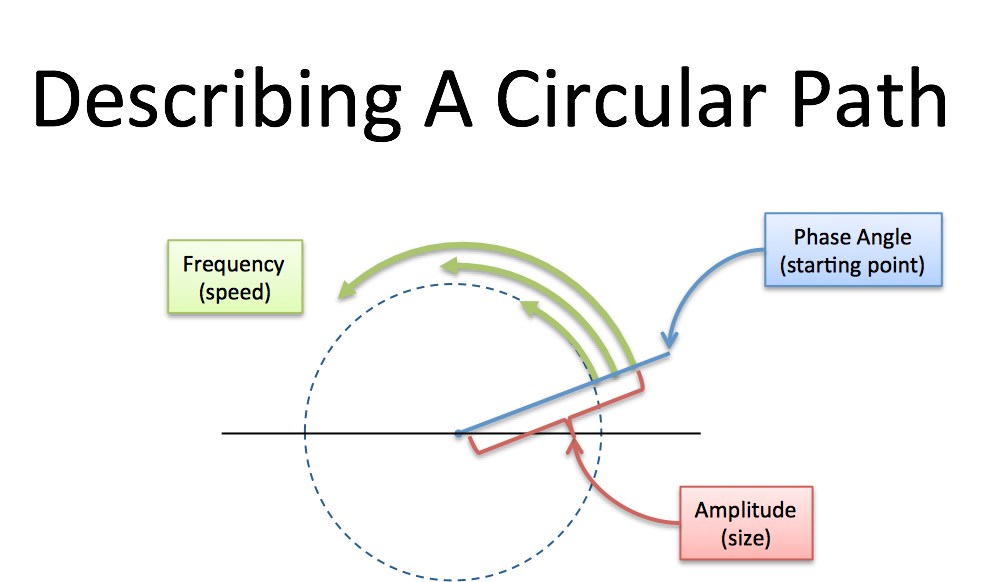
Following Circular Paths

Let's say we're chatting on the phone and, like usual, I want us to draw the same circle simultaneously. (You promised!) What should I say?

• How big is the circle? (Amplitude, i.e. size of radius)
• How fast do we draw it? (Frequency. 1 circle/second is a frequency of 1 Hertz (Hz) or 2*pi radians/sec)
• Where do we start? (Phase angle, where 0 degrees is the x-axis)

I could say "2-inch radius, start at 45 degrees, 1 circle per second, go!". After half a second, we should each be pointing to: starting point + amount traveled = 45 + 180 = 225 degrees (on a 2-inch circle).

Every circular path needs a size, speed, and starting angle (amplitude/frequency/phase). We can even combine paths: imagine tiny motorcars, driving in circles at different speeds.

The combined position of all the cycles is our signal, just like the combined flavor of all the ingredients is our smoothie.

Here's a simulation of a basic circular path:

(Based on this animation, here's the source code. Modern browser required. Click the graph to pause/unpause.)

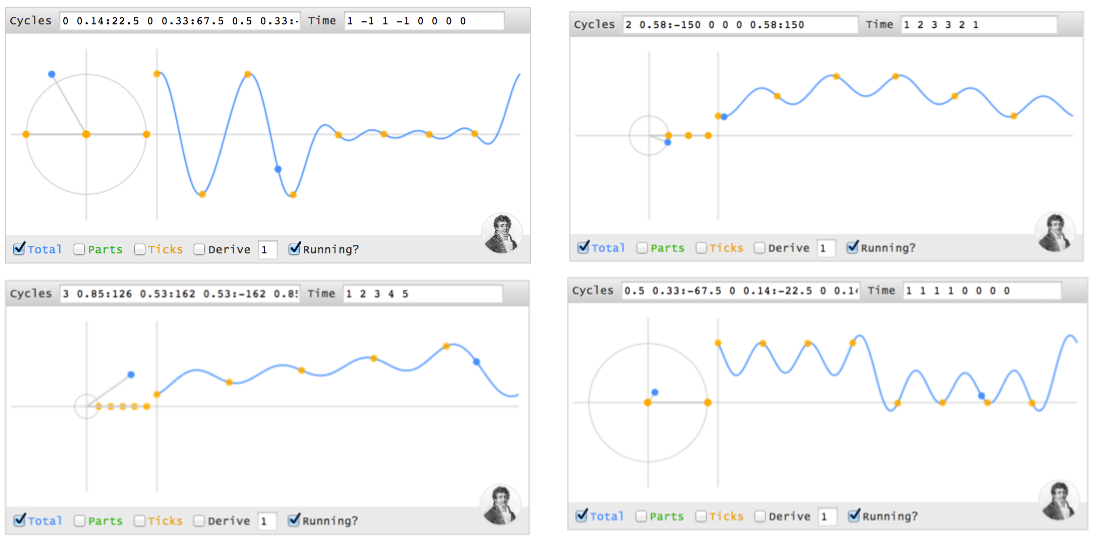
The magnitude of each cycle is listed in order, starting at 0Hz. Cycles [0 1] means

• 0 amplitude for the 0Hz cycle (0Hz = a constant cycle, stuck on the x-axis at zero degrees)
• 1 amplitude for the 1Hz cycle (completes 1 cycle per time interval)

Now the tricky part:

• The blue graph measures the real part of the cycle. Another lovely math confusion: the real axis of the circle, which is usually horizontal, has its magnitude shown on the vertical axis. You can mentally rotate the circle 90 degrees if you like.
• The time points are spaced at the fastest frequency. A 1Hz signal needs 2 time points for a start and stop (a single data point doesn't have a frequency). The time values [1 -1] shows the amplitude at these equally-spaced intervals.

With me? [0 1] is a pure 1Hz cycle.

Now let's add a 2Hz cycle to the mix. [0 1 1] means "Nothing at 0Hz, 1Hz of amplitude 1, 2Hz of amplitude 1":

Whoa. The little motorcars are getting wild: the green lines are the 1Hz and 2Hz cycles, and the blue line is the combined result. Try toggling the green checkbox to see the final result clearly. The combined "flavor" is a sway that starts at the max and dips low for the rest of the interval.

The yellow dots are when we actually measure the signal. With 3 cycles defined (0Hz, 1Hz, 2Hz), each dot is 1/3 of the way through the signal. In this case, cycles [0 1 1] generate the time values [2 -1 -1], which starts at the max (2) and dips low (-1).

Oh! We can't forget phase, the starting angle! Use magnitude:angle to set the phase. So [0 1:45] is a 1Hz cycle that starts at 45 degrees:

This is a shifted version of [0 1]. On the time side we get [.7 -.7] instead of [1 -1], because our cycle isn't exactly lined up with our measuring intervals, which are still at the halfway point (this could be desired!).

The Fourier Transform finds the set of cycle speeds, amplitudes and phases to match any time signal.

Our signal becomes an abstract notion that we consider as "observations in the time domain" or "ingredients in the frequency domain".

Enough talk: try it out! In the simulator, type any time or cycle pattern you'd like to see. If it's time points, you'll get a collection of cycles (that combine into a "wave") that matches your desired points.

But… doesn't the combined wave have strange values between the yellow time intervals? Sure. But who's to say whether a signal travels in straight lines, or curves, or zips into other dimensions when we aren't measuring it? It behaves exactly as we need at the equally-spaced moments we asked for.

Making A Spike In Time

Can we make a spike in time, like (4 0 0 0), using cycles? I'll use parentheses () for a sequence of time points, and brackets [] for a sequence of cycles.

Although the spike seems boring to us time-dwellers (one data point, that's it?), think about the complexity in the cycle world. Our cycle ingredients must start aligned (at the max value, 4) and then "explode outwards", each cycle with partners that cancel it in the future. Every remaining point is zero, which is a tricky balance with multiple cycles running around (we can't just "turn them off").

Let's walk through each time point:

• At time 0, the first instant, every cycle ingredient is at its max. Ignoring the other time points, (4 ? ? ?) can be made from 4 cycles (0Hz 1Hz 2Hz 3Hz), each with a magnitude of 1 and phase of 0 (i.e., 1 + 1 + 1 + 1 = 4).
• At every future point (t = 1, 2, 3), the sum of all cycles must cancel.

Here's the trick: when two cycles are on opposites sides of the circle (North & South, East & West, etc.) their combined position is zero (3 cycles can cancel if they're spread evenly at 0, 120, and 240 degrees).

Imagine a constellation of points moving around the circle. Here's the position of each cycle at every instant:

Time 0 1 2 3 
------------
0Hz: 0 0 0 0 
1Hz: 0 1 2 3
2Hz: 0 2 0 2
3Hz: 0 3 2 1

Notice how the the 3Hz cycle starts at 0, gets to position 3, then position "6" (with only 4 positions, 6 modulo 4 = 2), then position "9" (9 modulo 4 = 1).

When our cycle is 4 units long, cycle speeds a half-cycle apart (2 units) will either be lined up (difference of 0, 4, 8…) or on opposite sides (difference of 2, 6, 10…).

OK. Let's drill into each time point:

• Time 0: All cycles at their max (total of 4)
• Time 1: 1Hz and 3Hz cancel (positions 1 & 3 are opposites), 0Hz and 2Hz cancel as well. The net is 0.
• Time 2: 0Hz and 2Hz line up at position 0, while 1Hz and 3Hz line up at position 2 (the opposite side). The total is still 0.
• Time 3: 0Hz and 2Hz cancel. 1Hz and 3Hz cancel.
• Time 4 (repeat of t=0): All cycles line up.

The trick is having individual speeds cancel (0Hz vs 2Hz, 1Hz vs 3Hz), or having the lined-up pairs cancel (0Hz + 2Hz vs 1Hz + 3Hz).

When every cycle has equal power and 0 phase, we start aligned and cancel afterwards. (I don't have a nice proof yet -- any takers? -- but you can see it yourself. Try [1 1], [1 1 1], [1 1 1 1] and notice the signals we generate: (2 0), (3 0 0), (4 0 0 0)).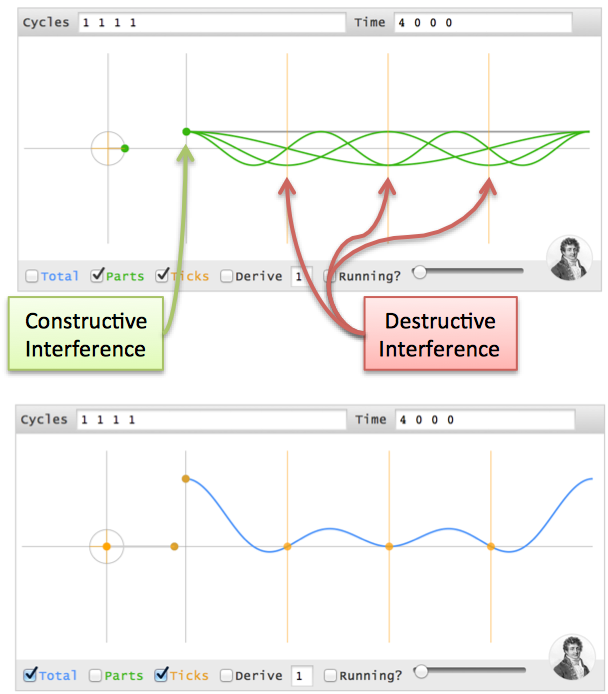

In my head, I label these signals as "time spikes": they have a value for a single instant, and are zero otherwise (the fancy name is a delta function.)

Here's how I visualize the initial alignment, followed by a net cancellation:

Moving The Time Spike

Not everything happens at t=0. Can we change our spike to (0 4 0 0)?

It seems the cycle ingredients should be similar to (4 0 0 0), but the cycles must align at t=1 (one second in the future). Here's where phase comes in.

Imagine a race with 4 runners. Normal races have everyone lined up at the starting line, the (4 0 0 0) time pattern. Boring.

What if we want everyone to finish at the same time? Easy. Just move people forward or backwards by the appropriate distance. Maybe granny can start 2 feet in front of the finish line, Usain Bolt can start 100m back, and they can cross the tape holding hands.

Phase shifts, the starting angle, are delays in the cycle universe. Here's how we adjust the starting position to delay every cycle 1 second:

• A 0Hz cycle doesn't move, so it's already aligned
• A 1Hz cycle goes 1 revolution in the entire 4 seconds, so a 1-second delay is a quarter-turn. Phase shift it 90 degrees backwards (-90) and it gets to phase=0, the max value, at t=1.
• A 2Hz cycle is twice as fast, so give it twice the angle to cover (-180 or 180 phase shift -- it's across the circle, either way).
• A 3Hz cycle is 3x as fast, so give it 3x the distance to move (-270 or +90 phase shift)

If time points (4 0 0 0) are made from cycles [1 1 1 1], then time points (0 4 0 0)are made from [1 1:-90 1:180 1:90]. (Note: I'm using "1Hz", but I mean "1 cycle over the entire time period").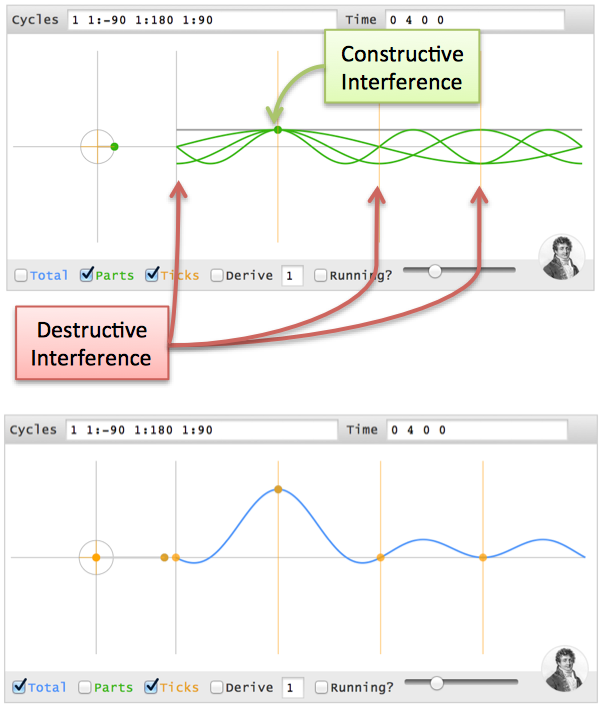

Whoa -- we're working out the cycles in our head!

The interference visualization is similar, except the alignment is at t=1.

Test your intuition: Can you make (0 0 4 0), i.e. a 2-second delay? 0Hz has no phase. 1Hz has 180 degrees, 2Hz has 360 (aka 0), and 3Hz has 540 (aka 180), so it's [1 1:180 1 1:180].

Discovering The Full Transform

The big insight: our signal is just a bunch of time spikes! If we merge the recipes for each time spike, we should get the recipe for the full signal.

The Fourier Transform builds the recipe frequency-by-frequency:

• Separate the full signal (a b c d) into "time spikes": (a 0 0 0) (0 b 0 0) (0 0 c 0) (0 0 0 d)
• For any frequency (like 2Hz), the tentative recipe is "a/4 + b/4 + c/4 + d/4" (the amplitude of each spike is split among all frequencies)
• Wait! We need to offset each spike with a phase delay (the angle for a "1 second delay" depends on the frequency).
• Actual recipe for a frequency = a/4 (no offset) + b/4 (1 second offset) + c/4 (2 second offset) + d/4 (3 second offset).

We can then loop through every frequency to get the full transform.

Here's the conversion from "math English" to full math:

A few notes:

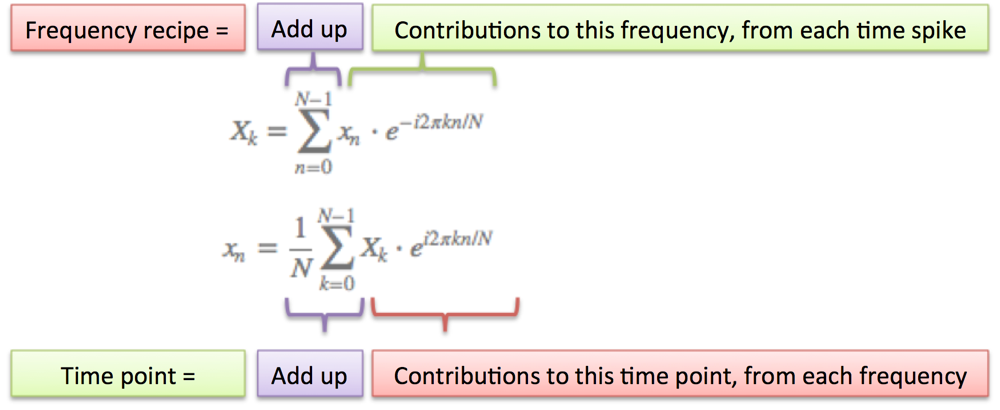
• N = number of time samples we have
• n = current sample we're considering (0 .. N-1)
• x_n = value of the signal at time n
• k = current frequency we're considering (0 Hertz up to N-1 Hertz)
• X_k = amount of frequency k in the signal (amplitude and phase, a complex number)
• The 1/N factor is usually moved to the reverse transform (going from frequencies back to time). This is allowed, though I prefer 1/N in the forward transform since it gives the actual sizes for the time spikes. You can get wild and even use [Math Processing Error]$1/\sqrt{N}$ on both transforms (going forward and back creates the 1/N factor).
• n/N is the percent of the time we've gone through. 2 * pi * k is our speed in radians / sec. e^-ix is our backwards-moving circular path. The combination is how far we've moved, for this speed and time.
• The raw equations for the Fourier Transform just say "add the complex numbers". Many programming languages cannot handle complex numbers directly, so you convert everything to rectangular coordinates and add those.

Onward

This was my most challenging article yet. The Fourier Transform has several flavors (discrete/continuous/finite/infinite), covers deep math (Dirac delta functions), and it's easy to get lost in details. I was constantly bumping into the edge of my knowledge.

But there's always simple analogies out there -- I refuse to think otherwise. Whether it's a smoothie or Usain Bolt & Granny crossing the finish line, take a simple understanding and refine it. The analogy is flawed, and that's ok: it's a raft to use, and leave behind once we cross the river.

I realized how feeble my own understanding was when I couldn't work out the transform of (1 0 0 0) in my head. For me, it was like saying I knew addition but, gee whiz, I'm not sure what "1 + 1 + 1 + 1" would be. Why not? Shouldn't we have an intuition for the simplest of operations?

That discomfort led me around the web to build my intuition. In addition to the references in the article, I'd like to thank:

• Scott Young, for the initial impetus for this post
• Shaheen Gandhi, Roger Cheng, and Brit Cruise for kicking around ideas & refining the analogy
• Steve Lehar for great examples of the Fourier Transform on images
• Charan Langton for her detailed walkthrough
• Julius Smith for a fantastic walkthrough of the Discrete Fourier Transform (what we covered today)
• Bret Victor for his techniques on visualizing learning

Today's goal was to experience the Fourier Transform. We'll save the advanced analysis for next time.

Happy math.

Appendix: Projecting Onto Cycles

Stuart Riffle has a great interpretation of the Fourier Transform:

Imagine spinning your signal in a centrifuge and checking for a bias. I have a correction: we must spin backwards (the exponent in the equation above should be [Math Processing Error]$e^{-i2\pi ...}$). You already know why: we need a phase delay so spikes appear in the future.

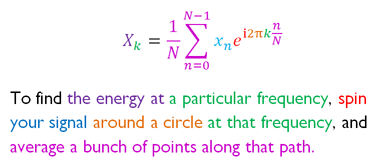
Appendix: Article With R Code Samples

João Neto made a great writeup, with technical (R) code samples here:

http://www.di.fc.ul.pt/~jpn/r/fourier/fourier.html

Appendix: Using The Code

All the code and examples are open source (MIT licensed, do what you like).

Source:https://betterexplained.com/articles/an-interactive-guide-to-the-fourier-transform

Time Series Analysis and Steps

TIME SERIES ANALYSIS: SHORT OVERVIEW

Steps in Time Series Analysis Modeling by edniel maratas 

What is Principal Component Analysis?

Introduction

The purpose of this post is to provide a complete and simplified explanation of Principal Component Analysis, and especially to answer how it works step by step so that everyone can understand it and make use of it, without necessarily having a strong mathematical background.

Before getting to the explanation, this post provides logical explanations of what PCA is doing in each step and simplifies the mathematical concepts behind it, like standardization, covariance, eigenvectors, and eigenvalues without focusing on how to compute them.

So what is Principal Component Analysis?

Principal Component Analysis, or PCA, is a dimensionality-reduction method that is often used to reduce the dimensionality of large data sets, by transforming a large set of variables into a smaller one that still contains most of the information in the large set.

Reducing the number of variables of a data set naturally comes at the expense of accuracy, but the trick in dimensionality reduction is to trade a little accuracy for simplicity. Because smaller data sets are easier to explore and visualize and make analyzing data much easier and faster for machine learning algorithms without extraneous variables to process.

So to sum up, the idea of PCA is simply — reduce the number of variables of a data set, while preserving as much information as possible.

Step by step explanation

Step 1: Standardization

The aim of this step is to standardize the range of the continuous initial variables so that each one of them contributes equally to the analysis.

More specifically, the reason why it is critical to perform standardization prior to PCA, is that the latter is quite sensitive regarding the variances of the initial variables. That is if there are large differences between the ranges of initial variables, those variables with larger ranges will dominate over those with small ranges (For example, a variable that ranges between 0 and 100 will dominate over a variable that ranges between 0 and 1), which will lead to biased results. So, transforming the data to comparable scales can prevent this problem.

Mathematically, this can be done by subtracting the mean and dividing by the standard deviation for each value of each variable.

Once the standardization is done, all the variables will be transformed to the same scale.

Step 2: Covariance Matrix computation

The aim of this step is to understand how the variables of the input data set are varying from the mean with respect to each other, or in other words, to see if there is any relationship between them. Because sometimes, variables are highly correlated in such a way that they contain redundant information. So, in order to identify these correlations, we compute the covariance matrix.

The covariance matrix is a p × p symmetric matrix (where p is the number of dimensions) that has as entries the covariances associated with all possible pairs of the initial variables. For example, for a 3-dimensional data set with 3 variables x, y, and z, the covariance matrix is a 3×3 matrix of this from:

Since the covariance of a variable with itself is its variance (Cov(a,a)=Var(a)), in the main diagonal (Top left to bottom right) we actually have the variances of each initial variable. And since the covariance is commutative (Cov(a,b)=Cov(b,a)), the entries of the covariance matrix are symmetric with respect to the main diagonal, which means that the upper and the lower triangular portions are equal.

What do the covariances that we have as entries of the matrix tell us about the correlations between the variables?

It’s actually the sign of the covariance that matters :
if positive then : the two variables increase or decrease together (correlated)
if negative then : One increases when the other decreases (Inversely correlated)

Now, that we know that the covariance matrix is not more than a table that summaries the correlations between all the possible pairs of variables, let’s move to the next step.

Step 3: Compute the eigenvectors and eigenvalues of the covariance matrix to identify the principal components

Eigenvectors and eigenvalues are the linear algebra concepts that we need to compute from the covariance matrix in order to determine the principal components of the data. Before getting to the explanation of these concepts, let’s first understand what do we mean by principal components.

Principal components are new variables that are constructed as linear combinations or mixtures of the initial variables. These combinations are done in such a way that the new variables (i.e., principal components) are uncorrelated and most of the information within the initial variables is squeezed or compressed into the first components. So, the idea is 10-dimensional data gives you 10 principal components, but PCA tries to put maximum possible information in the first component, then maximum remaining information in the second and so on.

An important thing to realize here is that the principal components are less interpretable and don’t have any real meaning since they are constructed as linear combinations of the initial variables.

Geometrically speaking, principal components represent the directions of the data that explain a maximal amount of variance, that is to say, the lines that capture most information of the data. The relationship between variance and information here, is that, the larger the variance carried by a line, the larger the dispersion of the data points along with it, and the larger the dispersion along a line, the more the information it has. To put all this simply, just think of principal components as new axes that provide the best angle to see and evaluate the data, so that the differences between the observations are better visible.

Step 4: Feature vector

As we saw in the previous step, computing the eigenvectors and ordering them by their eigenvalues in descending order, allow us to find the principal components in order of significance. In this step, what we do is, to choose whether to keep all these components or discard those of lesser significance (of low eigenvalues), and form with the remaining ones a matrix of vectors that we call Feature vector.

So, the feature vector is simply a matrix that has as columns the eigenvectors of the components that we decide to keep. This makes it the first step towards dimensionality reduction because if we choose to keep only p eigenvectors (components) out of n, the final data set will have only p dimensions.

Last step : Recast the data along the principal components axes

In the previous steps, apart from standardization, you do not make any changes on the data, you just select the principal components and form the feature vector, but the input data set remains always in terms of the original axes (i.e, in terms of the initial variables).

In this step, which is the last one, the aim is to use the feature vector formed using the eigenvectors of the covariance matrix, to reorient the data from the original axes to the ones represented by the principal components (hence the name Principal Components Analysis). This can be done by multiplying the transpose of the original data set by the transpose of the feature vector.

References :

[Steven M. Holland, Univ. of Georgia]: Principal Components Analysis

[skymind.ai]: Eigenvectors, Eigenvalues, PCA, Covariance and Entropy

[Lindsay I. Smith] : A tutorial on Principal Component Analysis

Chi-Square Analysis Test of Independence

Chi-Square Analysis 

Chapter Ix by edniel maratas on Scribd

CRITICAL VALUEb by edniel maratas on Scribd

Analysis of Variance (ANOVA)

DISCUSSION ON ANOVA 

Chapter Viii by edniel maratas on Scribd

CRITICAL VALUE 

F-ratio Table 2005 by edniel maratas on Scribd

What is Paired T-test and Proportion?

Test Concerning Means:Small Sample

Test on Small Sample (t-test)

          When the population standard deviation is unknown and the sample size is small, that is, less than 30, the t test is appropriate for testing hypothesis involving means. The formula is

Example 2: In order to increase customer service, a muffler repair shop claims its mechanics can replace a muffler in 12 minutes. A time management specialist selected six (6) repair jobs and found their mean time to be 11.6 minutes. The standard deviation of the sample was 2.1 minutes. At 0.025 level of significance, is there enough evidence to conclude that the mean time in changing a muffler is less than 12 minutes?

Solution: Follow the steps in hypothesis testing.

1. State the null and alternative hypothesis. Mathematically,

Ho: μ = 12 minutes

Ha: μ < 12 minutes 

2. Level of significance α = 0.025.

3. Select an appropriate test statistic.

The test statistic is the t– test, the sample size is less than 30 and the formula is

4. Determine the critical value and critical region

Since the level of significance is 0.025 and df = n – 1 = 6 – 1 = 5, and the alternative hypothesis is left – tailed test, then the critical value ( = -2.571.

Reject Ho, if t computed is less than -2.571.

5. Compute the value of the test statistics:

Given:

Sample mean = 11.6 minutes

Population mean = 12 minutes

Standard deviation = 2.1 minutes

Sample size = 6 samples

6. Decision: Since the computed t = -0.47 is in the acceptance region, thus, we fail to reject Ho.

7. Conclusion:

          Therefore, the data does not provide enough evidence to conclude that that the mean time in changing a muffler is less than 12 minutes.

Test Concerning Means:Large Sample

Test Concerning Means

One sample Case

          This case is concerned with only a single sample mean and we want to test the deviation of a sample mean from the population mean. Many hypotheses are tested using a statistical test based on the following formula:

Test Concerning Means: Large Sample (z-test)

Example 1: A manufacturer claims that the average lifetime of his lightbulbs is 3 years or 36 months. The standard deviation is 8 months. Fifty bulbs are selected, and the average lifetime is found to be 32 months. Should the manufacturer’s statement be rejected at 0.01 level of significance?

Solution: Following the steps in hypothesis testing we have

1. State the null and alternative hypothesis. Mathematically,

Ho: μ = 36 months (The average lifetime of lightbulbs is 36 months. Or the average lifetime of lightbulb is not different to 36 months)

Ha: μ ≠ 36 months (The average lifetime of lightbulbs is not equal to 36 months. Or the average lifetime of lightbulb is different to 36 months)

2. Level of significance α = 0.01.

3. Select an appropriate test statistic.

The test statistic is the z – test, the sample size is greater 30 and the formula is

4. Determine the critical value and critical region

Since the alternative hypothesis is nondirectional test, this illustration has two rejection regions one in each tail of the normal curve distribution of the sample mean. Thus, the equivalent critical value is z = ±2.58. Reject Ho if z > 2.58 or z < -2.58.

5. Compute the value of the test statistics:

Given:

Sample mean = 32 months

Population mean = 36 months

Standard deviation = 8 months

Sample size = 50 bulbs

6. Decision: Since the computed z = - 3.54 is in the rejection region, thus, reject Ho and accept Ha: μ ≠ 36 months

7. Conclusion:

Therefore, the average lifetime of lightbulbs in a certain manufacturing is not 36 months but in fact it is less than 36 months.